图形推理是行政职业能力测验试中一种非常重要的题型，几乎所有的公务员考试都要涉及到对图形推理的考查。由于图形推理不依赖于具体的事物，是一种公平的考试，更多体现的是考查考生的观察、抽象、推理能力。

　　由于图形本身变化多种多样，图形中可以设置规律的元素又非常多，所有很多考生会感觉不能一下子抓住解题的关键，对这类题目十分头疼。其实，要做好图形推理题目，首先要大量练习，提高对图形考查要素的敏感性，另外还要注意总结，发现一些常考规律的特征。在这里，我们就要介绍一种比较特殊的图形推理题目——等量代换题型。

　　所谓等量代换，意思就是将一种图形按某一数量比替换为另一种图形，然后再确定规律的题目。所以这类题目的特征是每个图形都是由几个小图形组成，小图形的种类数为两种或三种，而且单独某一种小图形的个数无规律，所有小图形的位置关系也无特殊规律。实际考试中只有两种小图形的题目较为多见，也相对容易发现规律，而三种小图形的就难一些，但在近几年的一些考试中出现较多，需加以注意。

　　一、两种小图形的等量代换题型

　　由于等量代换题目是将一种小图形按某一数量比替换为另一种小图形后形成数量上的规律，所以解题时最重要的是求出不同小图形之间的数量比然后进行替换。又由于替换后的数量规律通常为某种小图形个数都为n或呈等差数列，这两种情况下都可以按照连续三图的两边图形个数之和等于中间图形个数的2倍这一规律去计算，从而求得数量比。

　　例题1：

　　解析：题目中图形都是由圆和五角星两种小图形构成，而且单独的小图形个数无规律，考虑为等量代换题型。要去求得圆和五角星之间的数量比，按照规律计算，以前三图为例，第一图与第三图之和是2个五角星+4个圆，第二图的2倍也是2个五角星+4个圆，符合规律但是无法求出数量比，因此要换三个图计算。利用第二、三、四幅图计算，第二图与第四图之和为6个圆+2个五角星，第三图的2倍为4个五角星，两者相等可求得1个五角星等于3个圆，按这一数量比将图中的五角星都替换成圆，则圆的个数为4、5、6、7、8个，接下来一个图应为9个圆，观察选项发现D选项3个五角星正好等于9个圆。故答案选D。

　　二、三种小图形的等量代换题型

　　三种小图形的等量代换题型难度要大一些，因为要计算两种小图形和另一种小图形的数量比，而且这个数量比是不相同的，就需要寻找特殊的几个图，并仔细观察图形之间的变化趋势发现可能的规律，从而确定答案。

　　例题2：

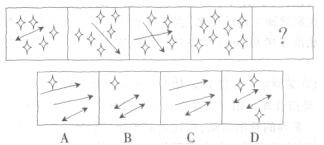
　　解析：题目中出现了三种小图形，分别是星星、双箭头和单箭头，且图形总数及单独一种小图形数量无规律，考虑为三种小图形的等量代换题目。通过观察发现这几个图中第四个图只有8个星星，那么就可以考虑将箭头都替换为星星寻找规律。而第一个图和第二个图分别为5个星星+1一个双箭头和6个星星+1个单箭头，如果将箭头转化为星星，先考虑最为简单的情况就是每个图星星个数相同，即都为8个，那么一个双箭头等于3个星星，一个单箭头等于2个星星，代入到第三个图发现正好符合，从而确定规律。故答案选A。

　　通过以上例题的讲解，希望考生们在学习过程中遇到图形推理问题能做到举一反三，事半功倍。

　　更多解题思路和解题技巧，可参看2017年公务员考试技巧手册。