“鸡兔同笼”是一类有名的中国古算题，出自我国1500年前唐代的一部算书《孙子算经》中。原题如下：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何?纵观近几年国家和各省地市公务员考试的数量关系题目很多都可以转化成这类问题，对于此类问题的解答要求考生熟练掌握。

　　大家想一下，这个题目是不是可以用这样的思路来想：鸡兔共有35只，如果把兔子的两只前脚用绳子捆起来，看作是一只脚，两只后脚也用绳子捆起来，看作是一只脚，那么，兔子就成了2只脚，即把兔子都先当作两只脚的鸡。鸡兔总的脚数是35×2=70(只)，比题中所说的94只要少94-70=24(只)。现在，松开一只兔子脚上的绳子，总的脚数就会增加2只，即70+2=72(只)，再松开一只兔子脚上的绳子，总的脚数又增加2……，一直继续下去，直至增加24，因此兔子数：24÷2=12(只)，从而鸡有35-12=23(只)。

　　我们来总结一下“假设法”的解题思路：先假设它们全是鸡，于是根据鸡兔的总数就可以算出在假设下共有几只脚，把这样得到的脚数与题中给出的脚数相比较，看看差多少，每差2只脚就说明有1只兔，将所差的脚数除以2，就可以算出共有多少只兔。此类我们称之为“假设法”，概括起来，解鸡兔同笼题的基本关系式是：

　　兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)

　　鸡数=(每只兔脚数×鸡兔总数-实际脚数)÷(每只兔子脚数-每只鸡脚数)

　　一、下面我们通过历年真题来进一步强化“假设法”

　　例1、某零件加工厂按工人完成的合格零件和不合格零件支付工资。工人每做一个合格零件得工资10元，每做一个不合格零件被扣除5元。已知某人一天共做了12个零件得工资90元。那么他在这一天做了多少个不合格零件?(　　 )(2008年国家公务员考试行测第54题)

　　A. 2　　　　B. 3　　　　C. 4　　　　D. 6

　　【答案】A　解析：本题中可令做一个合格零件得到的工资10元为兔脚，做一个不合格零件扣除的5元(即得到的-5元)为鸡脚，12个零件可以看作鸡兔总数，得到的工资90元可以看作鸡兔的总脚数，这样由解鸡兔同笼题的基本关系式可得：合格零件个数=(90-(-5×12))÷(10-(-5))=10个。不合格数为12-10=2个。(或利用公式计算不合格零件个数=(10×12-90)÷(10-(-5))=2个。)

　　例2、有大小两个瓶，大瓶可以装水5千克，小瓶可装水1千克，现在有100千克水共装了52瓶。问大瓶和小瓶相差多少个?(　　)(2009年浙江省公务员考试行测试卷)

　　A. 26个　　　B. 28个　　　C. 30个　　　D. 32个

　　【答案】B　解析：将大瓶装水量视为兔脚，小瓶装水量为鸡脚，则大瓶数为(100-1×52)÷(5-1)=12个，小瓶数为(5×52-100)÷(5-1)=40个。大瓶和小瓶相差40-12=28个。

　　以上是采用假设法解决“鸡兔同笼”的问题，但是数学中引入方程的思维，我们就可以把鸡兔同笼问题通过列二元一次方程进行求解。原题目是鸡头和兔头共有35个，鸡脚和兔脚共有94个，那我们就可以设鸡X只，兔子Y只。根据题目所给就可以列出一个简单的二元一次方程：.

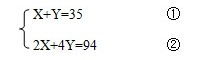
　　即：方程①鸡和兔子都是一个头，所以只数相加即是头的数量。方程②鸡两只脚，兔子四只脚，可以算出一共多少只脚。很简单的解方程问题。

　　二、下面我们通过2010年国家公务员考试真题来进一步强化“方程法”

　　例1、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?(　　)(2010年国家公务员考试行测第48题)

　　A.8　　　　B.10　　　　C.12　　　　D.15

　　【答案】D　解析：本题中可设甲教室举办X次培训，乙教室举办Y次培训，根据人数列方程，

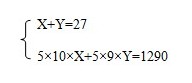
　　由方程我们可以得出题的答案。

　　例2、已知甲、乙两种产品原价之和为100元，因市场变化，甲产品8折促销，乙产品提价10%，价格调整之后，两种产品的标价之和比原标价之和提高了4%，则乙产品的原标价为多少元( )

　　A.20　　B.40　　C.80　　D.93

　　【答案】C　解析：本题中可设甲产品原价为X元，乙产品原价为Y元，根据甲乙标价之和前后比方程，

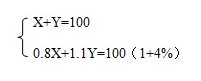
　　例3、某班35人外出春游，老师给了小明88元买冰激凌，买了两种口味，如果买20只巧克力味和15个草莓味的就差2元，买15个巧克力20个草莓的剩下3元，一只草莓味道的多少钱( )

　　A.4　　B.3　　 C.2　　D.1.5

　　【答案】C　解析：本题中可设巧克力味冰激凌为X元，草莓味冰激凌为Y元，列方程：

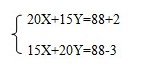
　　例4、有蜘蛛、蜻蜓、蝉三种生物共18只，共有腿118条，翅膀20对(蜘蛛8条腿，没有翅膀;蜻蜓有6条腿，2对翅膀;蝉有6条腿和1对翅膀)求蝉有几只?( )

　　A.5　　B.6　　 C.7　　D.8

　　【答案】B　解析：本题中可设蜘蛛X只，蜻蜓Y只，蝉Z只，列方程：

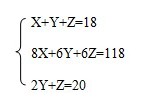
　　方程法解答鸡兔同笼问题比较直观，比如例4的题目涉及到三种物品时，假设法就很复杂了，但是采用方程法很简单的求出结果。

　　以上是关于鸡兔同笼问题的几种解题思路，从中找到适合自己的方式，并能将一般问题转化成鸡兔同笼问题是对考生的基本要求。

　　我个人倾向采用二元一次方程法解答鸡兔同笼问题，因为列方程的等式关系显而易见，并且不会出错，但是存在解方程费时的缺点。很多人认为采用“假设法”解答鸡兔同笼问题能在最短的时间里解出，但是存在需要记忆公式并解答的问题。所以希望考生们多做此类问题，找到适合自己的并能很快得出答案的方法。