行测这么多个题型中，对绝大多数考生而言，数学运算确实是一个让人比较头疼的题型。数学运算真的就那么难以突破？并不是的，其实它也有好搞定的点。今天永岸公考就集中将数学运算中大家必须要掌握的35个基础公式进行梳理。

　　工程问题：

　　工作总量=工作效率×工作时间

　　合作效率=多个人的效率之和

　　合作总量=合作效率×工作时间

　　经济利润问题：

　　利润=售价-成本

　　折扣=售价÷定价

　　利润率=利润÷成本

　　（注：数学运算中，除非特殊说明，利润率是用利润除以成本得到。但经济学方面、资料分析中利润率通常是利润÷营业收入）

　　总利润=单件商品利润×数量

　　容斥原理：

　　两集合容斥原理：A+B-A∩B=总数-都不

　　三集合容斥原理：A+B+C-（A∩B+B∩C+A∩C）+A∩B∩C=总数-都不

　　三集合变形公式：A+B+C-（“4”+“5”+“6”）-2×A∩B∩C=总数-都不

　　行程问题：

　　1.基础行程问题：

　　路程=速度×时间

　　平均速度=总路程/总时间

　　等距离平均速度=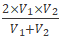

　　2.相遇追及问题：

　　两头分别出发的多次相遇问题：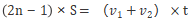

　　其中n代表相遇次数，S代表两地的距离，v1、v2代表两者的速度，t代表第n次相遇所用的时间。

　　一头同时出发的多次相遇问题：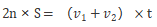

　　其中n代表相遇次数，S代表两地的距离，v1、v2代表两者的速度，t代表第n次相遇所用的时间。

　　追及问题：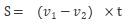

　　其中S代表两者开始追及时相距的距离，v1、v2代表两者的速度，t代表追上时所用的时间。

　　环形相遇问题：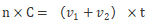

　　其中n代表环形相遇次数，C代表环形场地的周长，v1、v2代表两者的速度，t代表第n次相遇所用的时间。

　　环形追及问题：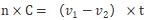

　　其中n代表环形追及次数，C代表环形场地的周长，v1、v2代表两者的速度，t代表第n次追上所用的时间。

　　3.流水行船问题：

　　顺流而下：路程=（船速+水速）×时间

　　逆流而上：路程=（船速-水速）×时间

　　顺流而下的速度-逆流而上的速度=2×水速

　　几何问题：

　　1.n边形的内角和与外角和：

　　内角和=（n-2）×180°；

　　外角和恒等于360°

　　2.平面方位图：

　　平面方位图始终遵循“上北下南左西右东”的作图原则，理解常见的表述，如：北偏东30°，代表从正北方向朝东偏30°的位置。

　　3.三角形相关理论：

　　三角形两边之和大于第三边，两边之差小于第三边；

　　直角三角形中，直角边的平方和等于斜边的平方；

　　相似三角形中，相似三角形对应角相等,对应边成比例。

　　排列组合：

　　1.排列相关：

　　排列是有顺序的，（a,b）与(b,a)是不同的排列。

　　公式：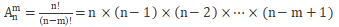

　　例：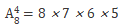

　　（从下标开始乘，乘以依次减1的上标那么多个数。此例子即为从8开始乘，乘以依次减1的4个数。）

　　2.组合相关：

　　组合是无顺序的，（a,b）与(b,a)是相同的组合。

　　公式：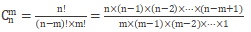

　　例：

　　公式：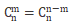

　　例：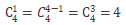

　　3.加法原理与乘法原理：

　　分类用加法，

　　分步用乘法。

　　概率相关：

　　概率=满足条件数/总情况数；

　　分步概率=各步概率的乘积；

　　分类概率=各类概率的和。

　　浓度问题：

　　溶液=溶质+溶剂；

　　浓度=溶质÷溶液；

　　混合溶液浓度=混合前溶质之和÷混合前溶液之和

　　钟表问题：

　　一个指针走完一圈360°，一个表盘360°；总共分为12个大格和60个小格；1个大格等于30°，1个小格等于6°；

　　时针每分钟走0.5°，分针每分钟走6°，速度差为5.5°/分，速度之比为12：1；

　　时针与分针每小时出现2次直角，1次重合，一次180度；时针与分针每昼夜出现44次直角，22次重合，22次180度。

　　牛吃草问题：

　　基础公式：y=(N-x)×t，其中y代表原草量，N代表牛的头数，x代表草生长的速度，t代表牛吃完这片草所用的时间。

　　植树问题：

　　单边线形植树公式（两端都植）：棵数=总长÷间隔+1；

　　单边楼间植树公式（两端都不植）：棵数=总长÷间隔-1；

　　环形植树公式：棵数=总长÷间隔；

　　数学运算中常考的这些基础公式，并不复杂，只是涉及的知识点是比较多，看起来有点难。需要做的就是将不同考点的各个公式中的字母、概念，如何与题干中的文字一一对应上，并能写成数学关系式。

　　这一点搞定，再通过练题将它们熟练掌握，做到心中有数，这样才能在最后十分钟的时间内做对那50%的简单题，让数学运算成为自己提分的一个小突破口，整体提升自己的行测分数。